Revisão 5ª série

1 – Decomponha os números em fatores primos:

180 -                  220  -               320  -               308 -                 605 -              

616 -                1008 -              1210 -               2058 -              3125 -            

4225 -              5040 -




2 – Qual é o número cuja fatoração é:
 a) 2 . 2. 3 . 5 . 7
b) 3 . 3 . 5 . 5 . 7.
c) 2 . 3 . 5 . 7
d) 5 . 5 . 11 . 13

3 – Dos números abaixo, quais deles são divisíveis por 2, 3, 4, 5, 6, 9 e 10.

16 -          128 -                 287 -                1006 -           43 -                   265 -

480 -        4785 -               76 -                 342  -             632 -                8335 -

82 -           231 -               700  -               5000 -           2556 -               160 -

 OBS : Usem os criterios de divisibilidade



                                  Divisores de um número

Divisores de um número natural são todos os números naturais que ao dividirem tal número, resultarão em uma divisão exata, isto é, com resto igual a zero.
O conjunto dos divisores de um número é um conjunto finito, mas como determinar quantos divisores um número natural possui?
Tanto para a identificação da quantidade de divisores de um número, assim como para que possamos encontrar tais divisores, iremos recorrer à fatoração ou decomposição em fatores primos.
Tomemos como exemplo o número 200 para aprendermos a identificar quantos e quais são os seus divisores.

Fatorando

Primeiramente iremos decompor o número 200 em fatores primos:

Temos então que 200 fatorado é igual a 2³ . 5².

Quantidade de Divisores de um Número Natural

O número 200 decomposto possui dois fatores primos. Um com expoente 3 (2³) e outro com expoente 2 (5²). A multiplicação destes expoentes adicionados em uma unidade cada um deles, irá nos fornecer a informação procurada:
(3 + 1) . (2 + 1) = 12
Portanto o número natural 200 possui um total de 12 divisores naturais.

Conjunto dos Divisores de um Número Natural

Mas quais são estes 12 divisores naturais do número 200? Analisemos a figura abaixo: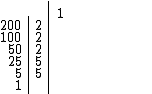

Notamos que à direita da fatoração do número 200, executada mais acima no início deste tópico, foi traçada uma outra linha vertical e colocado o número 1 no topo. Ele foi considerado, pois todos os números naturais são divisíveis por ele.
Temos então que { 1 } é o primeiro subconjunto obtido dos divisores de 200.
A partir daí, todos os outros divisores serão obtidos através da multiplicação do fator da linha em questão, por todos os divisores das linhas acima, até então calculados, ou em outras palavras, obtidos através da multiplicação do fator da linha em questão por todos os elementos do atual subconjunto de divisores, mas há uma exceção: Quando o fator da linha em questão for igual ao fator da linha anterior, ao invés de o multiplicarmos por todos os divisores já encontrados, o multiplicamos apenas pelos divisores encontrados na linha anterior, pois caso contrário iremos obter vários divisores que já foram encontrados anteriormente. Se quisermos seguir a regra geral, o único problema, além do desperdício de tempo, é que teremos que eliminar as duplicidades, considerando cada divisor apenas uma vez.
Multiplicando-se o primeiro fator 2 por cada elemento do subconjunto atual (2 . 1 = 2), obteremos o novo subconjunto { 1, 2 } que conta agora com dois divisores.

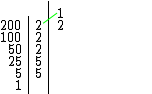
Multiplicando-se o segundo fator 2 por cada elemento do subconjunto atual (2 . 1 = 2, 2 . 2 = 4), obteremos um novo subconjunto { 1, 2, 4 }, que conta agora com três divisores. Podemos notar que o divisor 2 que já fazia parte do subconjunto anterior foi considerado apenas uma vez.

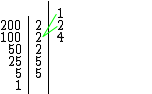
Neste caso poderíamos ter calculado apenas o produto (2 . 2 = 4), pois o fator 2 em questão é o mesmo fator da linha anterior, então o multiplicamos apenas por 2, que é o único divisor encontrado na linha anterior, evitando assim a perda de tempo em cálculos que resultarão em valores já obtidos.
Como o terceiro fator 2 é novamente uma repetição do fator acima, vamos apenas multiplicar (2 . 4 = 8), obtendo o novo subconjunto { 1, 2, 4, 8 }, que conta agora com quatro divisores. Note que se tivéssemos multiplicado por todos os divisores acima, encontraríamos 2 e 4 em duplicidade.

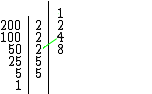
Multiplicando-se o primeiro fator 5 pelos elementos do subconjunto atual (5 . 1 = 5, 5 . 2 = 10, 5 . 4 = 20, 5 . 8 = 40), obteremos um novo subconjunto { 1, 2, 4, 5, 8, 10, 20, 40 }, que conta agora com oito divisores.

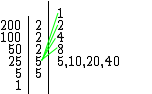
Finalmente multiplicando-se o segundo fator 5 pelos elementos da linha acima, já que ele se repete, (5 . 5 = 25, 5 . 10 = 50, 5 . 20 = 100, 5 . 40 = 200), obteremos um novo subconjunto { 1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 200 }, que conta agora com os doze divisores de 200 como já era de se esperar.

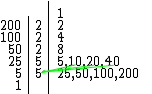
Portanto os doze divisores naturais de 200 são: 1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100 e 200.
                                                                                  (Matematica Didatica)


4 - Encontre os divisores dos números:

a) 48 -

b) 40 -

c) 120 -

d) 78 -


   Bom estudo